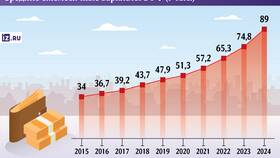
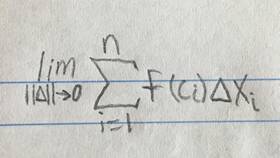Сумма бесконечной геометрической прогрессии - это предельное значение суммы ее членов при неограниченном возрастании их количества. Данная величина существует только при определенных условиях и имеет важное значение в математическом анализе и прикладных науках.
Содержание
Условия существования суммы
Сумма бесконечной геометрической прогрессии существует только когда модуль знаменателя прогрессии |q| меньше 1:
- При |q| ≥ 1 сумма расходится (не существует)
- При |q| < 1 сумма сходится к определенному значению
Формула суммы бесконечной прогрессии
Для бесконечной геометрической прогрессии с первым членом b₁ и знаменателем |q| < 1 сумма вычисляется по формуле:
| S = | b₁ | , где |q| < 1 |
| 1 - q |
Примеры вычислений
- Для прогрессии 1 + 1/2 + 1/4 + 1/8 + ...:
- b₁ = 1, q = 1/2
- S = 1 / (1 - 1/2) = 2
- Для прогрессии 9 - 3 + 1 - 1/3 + ...:
- b₁ = 9, q = -1/3
- S = 9 / (1 - (-1/3)) = 27/4 = 6.75
Геометрическая интерпретация
| Пример | Геометрическая модель |
| 1 + 1/2 + 1/4 + 1/8 + ... = 2 | Деление отрезка пополам бесконечное число раз |
| 0.9 + 0.09 + 0.009 + ... = 1 | Доказательство равенства 0.(9) = 1 |
Применение в различных областях
- В экономике: расчет бесконечных денежных потоков
- В физике: анализ затухающих колебаний
- В компьютерных науках: оценка сложности алгоритмов
- В теории вероятностей: вычисление математических ожиданий
Сумма бесконечной геометрической прогрессии представляет собой важный математический инструмент, позволяющий работать с бесконечными процессами в конечных величинах. Понимание этого концепта необходимо для решения широкого круга задач в высшей математике и ее приложениях.